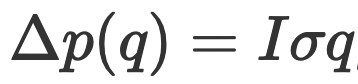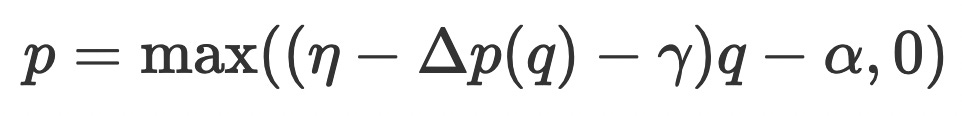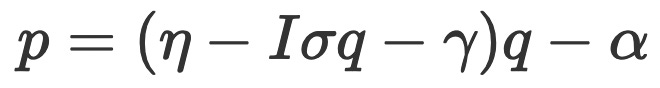Arcadia Collateral Risk Simulation: Progress Report 1
The first in a series of updates on the joint project by Llama Risk and Pragma Labs for the Arcadia v2 protocol.
Introduction
Llama Risk and Pragma Labs initiated a partnership on January 8th to enhance the economic security of the upcoming Arcadia V2 Protocol (See the announcement post here). Our project involves co-developing a customized ABS/statistical model of Arcadia that will enable parameterization of the Lending Module through simulation-based methodology. This tool will be used to onboard collateral types and is generalized to support a variety of assets, including ERC-20s, ERC-4626s, and LP tokens.
This post is the first of a multi-part series that will cover our progress on the simulation project for the benefit of the Arcadia community and other DeFi protocols interested in developing tools that help identify and minimize the risk of bad debt to the protocol. We've divided the post into 3 sections:
Section 1: Arcadia Protocol V2 - We give an overview of the Arcadia Protocol which informed us of the required simulation components.
Section 2: The Simulation - We define the parameters, success metrics, and goals of the simulation. We then explain the simulation methodology.
Section 3: Current State of the Project - We provide a brief update on the current state of the project.
Section 1: Arcadia Protocol V2
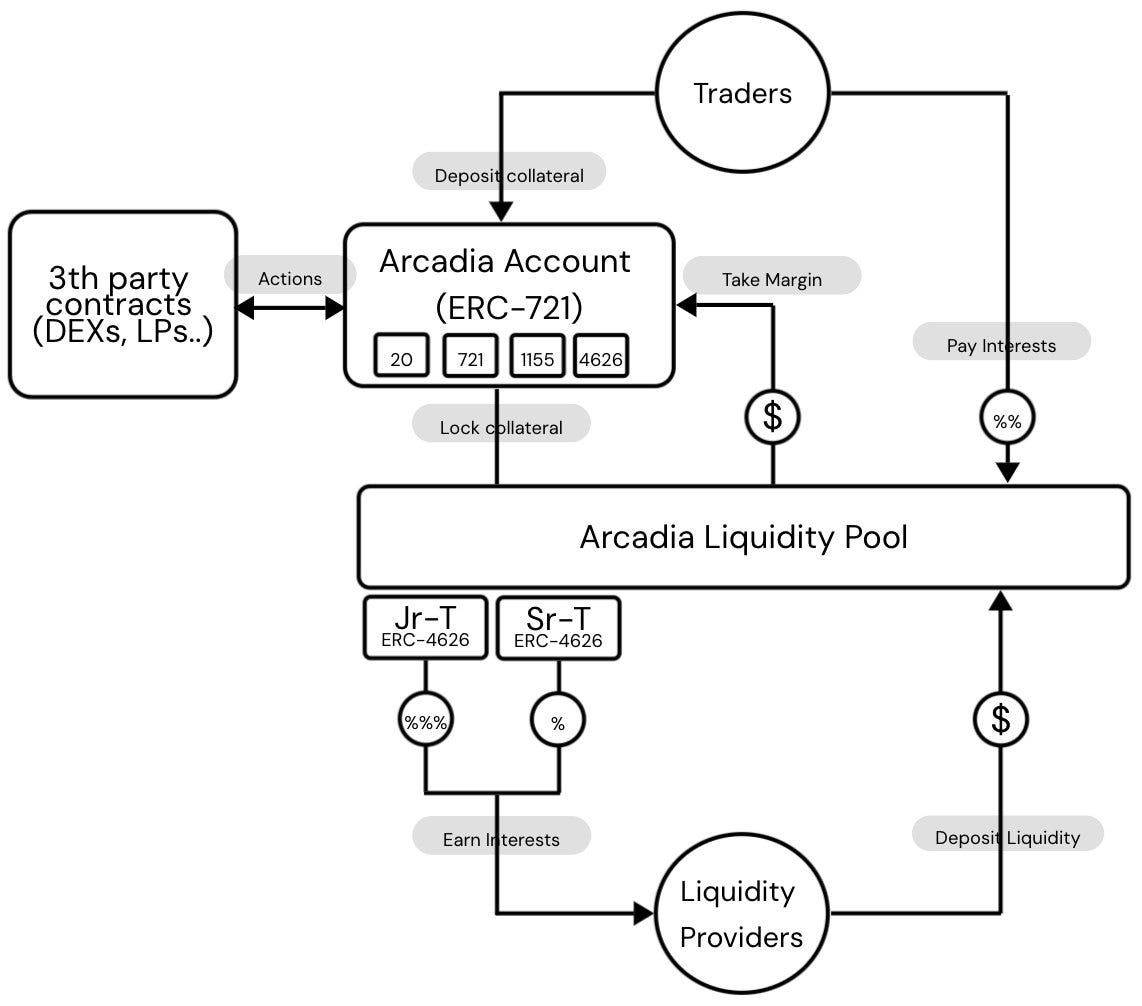
Arcadia is a non-custodial platform for asset management through lending and margin accounts. Arcadia Protocol gives users an on-chain account with which they access margin credit by providing a portfolio of assets as collateral. Core to this functionality is the Arcadia Lending Module.
How does Arcadia Lending work?
On a conceptual level, Arcadia consists of a two-sided lending market between liquidity providers and borrowers:
Liquidity Provider: Arcadia Lending relies on liquidity pools, where Liquidity providers deposit capital into the pools and earn interest paid on loans. Arcadia offers, initially, two risk tiers through two types of tokens, Junior Tranche (Jr-T) and Senior Tranche (Sr-T), which represent different risk-reward profiles for Liquidity Providers.
Borrowers: Borrowers can deposit a range of assets (ERC-20, ERC-721, ERC-1155, ERC-4626) into an Arcadia Account (represented as an ERC-721), locking them as collateral to take out loans in exchange for interest. The account locks a specific value, not individual assets, and the owner can actively manage the assets within the account as long as the total value remains above the collateralization threshold.
The interaction between these two parties is facilitated through the Arcadia Lending Contract. These providers earn interest by depositing liquidity into the lending pool. The flow of funds and interactions between the participants in the protocol is represented by the arrows in the above diagram.
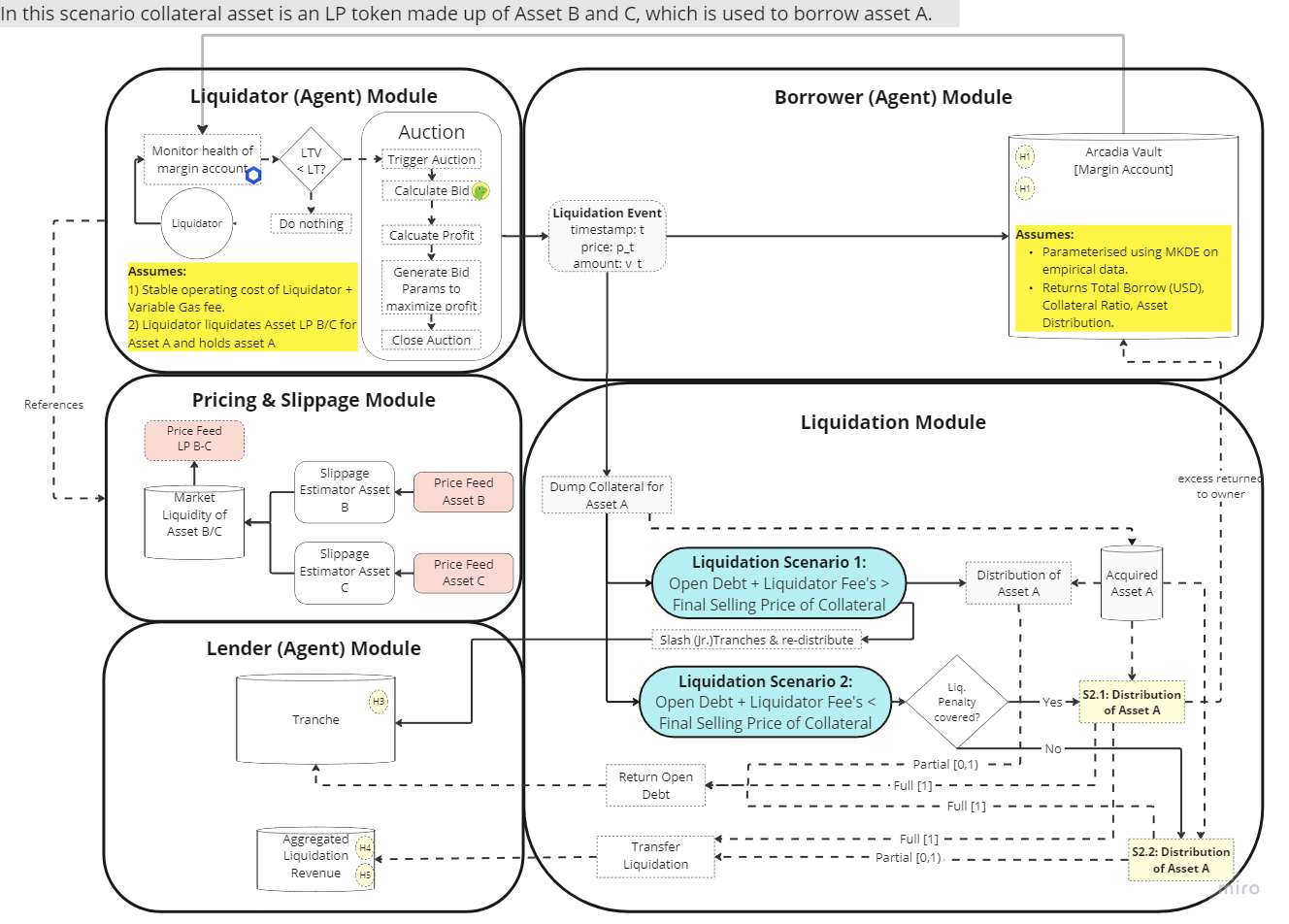
Liquidations
Liquidation within Arcadia's system is conducted via a three-step process using a Gradual Dutch Auction. Initially, anyone can initiate the liquidation of an account that falls below the health threshold, receiving a reward for doing so. The auction that follows sees the account's price gradually decrease until a buyer, typically an MEV searcher looking to minimize slippage, intervenes and places a bid. The process allows for partial liquidations to reduce market impact. Post-liquidation, during the closing of the auction, the outcome depends on the final selling price relative to the debt and liquidation penalties, with possible allocations to the protocol’s treasury, risk tranches, or back to the account owner.
In Arcadia's liquidation process, there are three scenarios after an account is sold:
If the selling price is less than the debt, the shortfall is covered by the junior risk tranche's tokens.
If the selling price exceeds the debt but is under the debt plus liquidation penalty, the surplus is shared between Arcadia's treasury and the junior tranche.
If the selling price surpasses the debt and the liquidation penalty cap, excess funds after penalty distribution are returned to the account's original owner.
Collateral Evaluation
Arcadia, similar to other large lending protocols, operates with an allow list of what assets can be used as collateral. This is essential as collateral types differ in their market risk (i.e. liquidity and volatility) and counterparty risk (i.e. decentralization).
Consider a hypothetical asset that is highly volatile and illiquid. If such an asset were accepted as collateral within a protocol like Arcadia, it could lead to unstable credit markets. For instance, if the asset's price suddenly drops due to its volatility, it might not be sold quickly enough to cover a loan in the event of a liquidation due to its illiquidity. This could result in losses for the protocol and its lenders.
Yet, a broader question can be asked, then: what asset should be listed? If an asset is on the allow list, under what conditions should liquidation of this asset occur that will maximize the protocol's potential for growth without introducing an undue risk of bad debt? This leads to the fundamental answer that the risk simulation should provide.
The Simulation
The engagement between Llama Risk and Pragma Labs aims to develop a simulation tool that will emulate historical price and liquidity scenarios in the market. These primary exogenous risks to Arcadia can be summarized as follows:
Risk 1: Shocks to market prices of collateral that cause the protocol to become insolvent due to undercollateralization
Risk 2: Loss of liquidity in an external marketplace, leading to a liquidator being disincentivized to liquidate defaulted collateral.
The simulation tool's purpose is to assign optimal parameters that maximize protocol revenue while minimizing the occurrence of bad debt by tuning the following parameters:
Collateral Factor: Identifying the ideal value or range of values that balances a collateral's volatility with an optimal borrowing capacity.
Liquidation Factor: Establishing a threshold attractive to borrowers that effectively manages asset liquidation without exacerbating risks.
Exposure: Defining the extent of exposure to a collateral type, given its liquidity profile, such that there is an assurance of protocol stability in anticipated market conditions.
These parameter optimization aims to achieve the following outcomes:
Minimize protocol bad debt for Arcadia
Minimize risk for Junior tranches
Maximize protocol revenue for Arcadia
Defining Simulation "Success" Metrics
To optimize the parameters outlined within our simulation, we are adapting and extending the "success" criteria of a successful simulation run proposed by Fu et al. (2021). The criteria can be summarized as follows:
Net Insolvent Value Percentage of the Entire Protocol: Measures the total insolvency risk by comparing the net insolvent values of all accounts to the total collateral value. It is considered "safe" if the value within the simulation remains below 1%. (See H1)
Asset Net Insolvent Value Percentage: Provides a detailed view of insolvency by calculating the net insolvent value for specific assets, adjusted by the pro-rata supply percentage, and comparing it to the total collateral value of those assets. A threshold of 5% has been set as the failure criterion for each asset. (See H2)
Slashing Run Percentage: Evaluates the protocol's financial resilience by determining the percentage of simulation runs that result in a significant reduction of the Total Tranche's value due to insolvencies. A safety breach is indicated if more than 1% of the Total Tranche's total value is slashed to cover insolvencies. (See H)
Additionally, in line with our objective to optimize profitability, the following metrics are tracked:
Net Protocol Revenue: The aggregate financial gain from liquidation profits and interest income across all borrowed assets, representing the total profitability of the lending protocol.
Net Protocol Revenue per Asset: This metric calculates the financial gain from liquidation profits and interest income for each specific asset within the lending protocol, offering insight into the profitability contributed by individual assets.
Arriving at a Parameter Recommendation
We will run simulations with different parameters (i.e. Collateral Factor, Liquidation Factor, and Debt Ceiling) in a grid search with early stopping mechanics. This means we will have a set of parameters for which we will run each possible combination.
Each parameter combination will have 30 runs to achieve statistical significance and a wide range of borrower distributions. We will then compare after each simulation run if the criteria of safety (i.e. net insolvent < 1%, Asset Net Insolvent < 5%, slashing pct < 1%) have been met and what the respective Net Protocol Revenue and Net Protocol per Asset are. The recommended parameter choice will be the one that meets the safety criteria and achieves the highest Revenue metrics.
Simulation Methodology
Agents in the simulation periodically check the current status of environmental variables. Their actions at any given moment and situation are determined by a predefined policy. Each time an agent takes an action, the simulation setting processes these actions, leading to updates of the simulation state.
Sampling
For each set of parameters, we run the simulation 30 times (i.e. in line with the Central Limit Theorem) to make sure that the sample size is large enough to cover a wide range of borrowing distributions (Morrow et al., 2020; Fu et al., 2021).
Simulation Duration
The simulation time will span approximately 24 hours, with a re-parameterization of relevant parameters (i.e. borrower portfolios) following each step. This approach is designed to reflect empirical data accurately, as it allows a balance between capturing significant price movements and accommodating potential adjustments in borrower behavior. This method aligns with the methodologies previously employed by Kao et al., 2020; Morrow et al., 2020; Fu et al., 2021 and Chaudhary & Pinna, 2022.
Asset Price Trajectory
The Arcadia simulation will utilize historically observed price data of the respective assets. Given that Arcadia relies on Chainlink Oracles, we will utilize the price from the Oracles and not the market price for triggering liquidation. The liquidator, however, will reference the market price. Standard implementations usually employ Geometric Brownian motion (GBM) to simulate price trajectories (see for instance Morrow et al., 2020). However, we leave this to future work.
Slippage & Liquidity
We have fitted a slippage model to estimate slippage on a trade that incorporates both linear and exponential models to accurately represent the dynamics of slippage within the cryptocurrency market. We fitted the curve using on-chain data of the most liquid pool pair. This framework is a direct response to the insights provided by Kao et al. (2020), who found that linear relationships, exemplified by the formula:
, offer a more precise approximation of slippage effects compared to traditional square-root models. Our implementation expands upon this by also integrating exponential models for certain token pairs, reflecting the nuanced liquidity conditions across different cryptocurrency exchanges. This dual-model approach allows us to account for the variability in slippage behavior, acknowledging that, in contrast to traditional financial markets, slippage in cryptocurrency markets can significantly increase with larger orders due to inherently lower liquidity.
Agents
For the Simulation, we require three different agents - borrower, liquidator, and liquidity provider. Practically, in this simulation we limit empirical parameterization to the Borrower only.
Parameterizing Borrower
The initial approach for Arcadia involves parameterizing borrower behavior using empirical data extracted from similar protocols and major lending platforms and Arcadia v1 Data. In line with DeFi simulation practices, passive borrower agents will be employed, meaning they won't adjust their portfolio based on market conditions but will maintain their initial parameters. The inclusion of active agents, adapting to market conditions, is reserved for future work.
To parameterize borrowers, methods similar to Morrow et al. (2020) will be used, sampling collateral value and collateralization ratios from real-world distributions. The process involves loading borrower data, applying multivariate kernel density estimation, adjusting under-collateralized data points, and rescaling the samples to match the simulation input while maintaining the processed data for simulation.
Implied Lenders
Lenders in the simulation are not directly parameterized. The simulation operates under the assumption that borrowers, which have been parameterized on empirical data, had sufficient liquidity to open their positions. In line with Morrow et al., (2020), the total amount of a given unit of asset supplied by lenders in the simulation is set to equal the sum of all borrowers’ total outstanding debt plus an additional unit of a given unit of asset (i.e., total outstanding debt + 1). In simpler terms, when we set up a borrower in our simulation, we're assuming there's enough money available for them to borrow what they need.
Parameterizing Liquidators
A rational liquidator primarily aims to maximize profits by ensuring that the revenue from liquidation incentives outweighs the costs. The cost model assumes the liquidator submits a market order on a DEX, providing a worst-case cost estimate. The profit
of each trade is calculated as:
Where η is the liquidation incentive, γ the trading fee, and α the transaction fee.
Liquidation Strategy
For each liquidation opportunity, the liquidator repays the minimum of the following:
Value of borrower’s liquidatable collateral.
Liquidator agent’s perceived optimal repay amount.
Optimal Liquidation Amount
To derive the optimal repayment amount for maximizing profit, we incorporate the slippage model into the profit function. (Note: If we employ the share root model we simply replace the linear root model.) For a linear slippage model, the profit function is:
Maximizing profit involves finding the derivative of the profit function with respect to the normalized order size q and solving for q* where ∂qp(q*)=0. This value q* represents the optimal order size for maximizing net profit.
Time Preferences of Liquidators
For simplicity and safety, it's assumed that liquidators immediately sell their acquired collateral. While this may seem like a simplification, it aligns with the expected outcome of a profit-maximizing strategy as documented in Morrow et al., 2020, irrespective of the valuation of the collateral asset.
Section 3: Current State of the Project
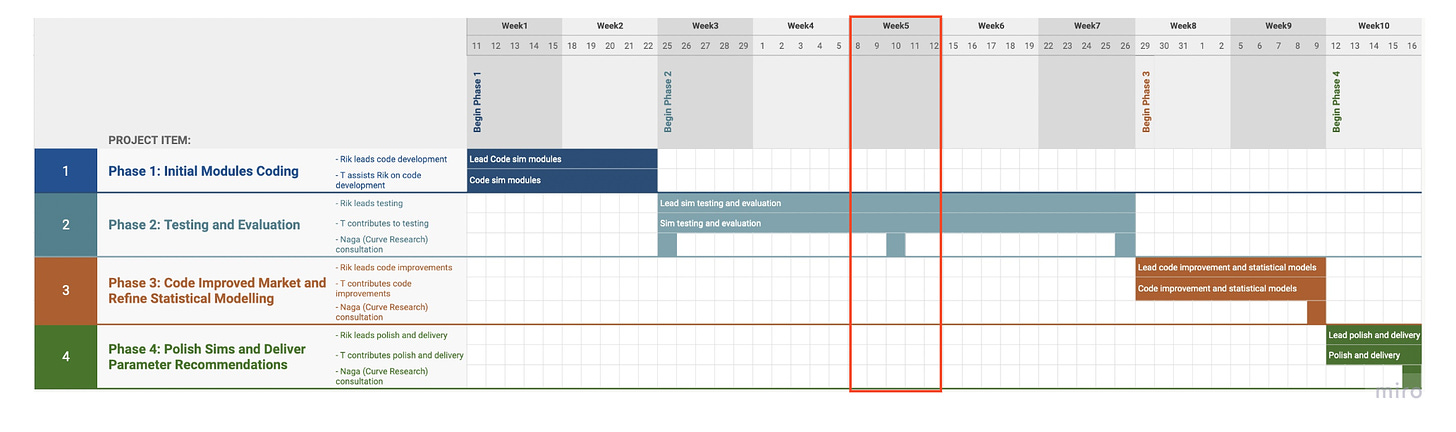
The project thus far has successfully navigated through its planned phases, achieving all set milestones with notable accomplishments.
In Phase 1, the Coding of the Initial Modules, the team dedicated two weeks to the development of key components including the Market Module, Backstop Module, Liquidator Module, and Liquidation Engine Module. This foundational work was carried out in a joint effort by the Pragma Labs Risk lead and Llama Risk team.
The functional model set the stage for Phase 2, Testing and Evaluation. The project has now entered a critical five-week period focused on assessing the model's performance under simulated conditions. The team, now augmented by insights from the Curve Research team and with the support of Arcadia's Risk Lead, undertakes a comprehensive evaluation of the model.
In line with Kleijnen (1995), this phase consists of
verification of the model (i.e. determining that a simulation computer program performs as intended), and
validation of the model (i.e. determining whether the conceptual simulation model (as opposed to the computer program) is an accurate representation of the system under study).
Thus far, the majority of the focus has been on the verification of the model. Uncovered problems have been continuously fixed by the team. This phase is marked by an iterative process between testing and refinement.
The goal by the end of the week is to have realistic scenarios implemented to start focusing on model validation.
Next Week’s Post:
Next week we will dive deeper into the simulation itself and give further updates on the weekly progress.
References:
Chaudhary, Amit, and Daniele Pinna. ‘A Multi-Asset, Agent-Based Approach Applied to DeFi Lending Protocol Modelling’. arXiv, 14 December 2022. http://arxiv.org/abs/2211.08870.
Fu, W., Chitra, T., Chiang, R., & Morrow, J. (2021). An analysis of the financial risk to participants in the Aave V1 and V2 protocols. https://gauntlet.network/reports/aave
Kao, H.-T., Chitra, T., Chiang, R., & Morrow, J. (2020). An Analysis of the Market Risk to Participants in the Compound Protocol.
Kleijnen, J. P. (1995). Verification and validation of simulation models. European journal of operational research, 82(1), 145-162.
Morrow, J., Chiang, R., Chitra, T., & Kao, H.-T. (2020). An analysis of the financial risk to participants in the Compound protocol. https://gauntlet.network/reports/compound
Disclaimer: Any Materials presented here might change with the uncovering of new insights during simulation validation and verification.